| Home |
| People |
| Papers |
| Tool Description |
Our algorithm was implemented in Java and is called LOBACS. This stands for LOwer Bound Approximation Counting Satisfiability). Our implementation can be freely downloaded for evaluation here. Table 1 shows the execution times and the value of the number of solutions (exact with Cachet) and lower bound (with LOBACS). We have used two kinds of tests: some small instances from the SATLIB benchmark, and some larger instances with more variables and clauses which we randomly generated. Both tools were run on Red Hat Linux 9.0 with a Pentium 4, 2.4 GHz processor which has 512 MB of memory.
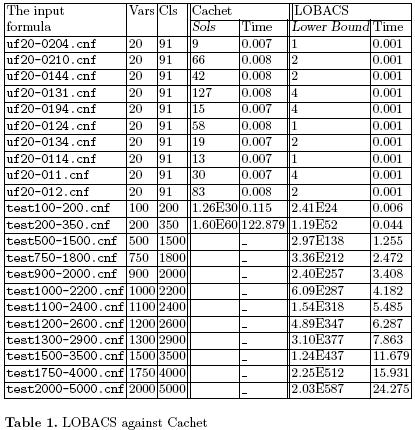
The timings are given in seconds, and the symbol in Table 1 means that Cachet was unable to provide the answer in less than three days (i.e., the default Cachet timeout). The “Input” column of Table 1 contains a list of formulæ from the class uf20, downloaded from the Web site of SATLIB. The class of propositional formulæ test were randomly generated by us. The next two columns denote the number of variables and columns of the respective input formulæ. The last four colums show the number of truth assignments (Sols) and the execution times (expressed in seconds) done by Cachet and LOBACS, respectively. Table 1 demonstrates that LOBACS outperforms Cachet with a order of magnitude between 7 and 2700. The reason is due to the fact that Cachet is an exact counting SAT solver, whereas LOBACS is an approximation. Our preliminary results show that the approximation is quite reasonable, the lower bound is of similar magnitude to the exact count for the larger problems. Clearly there is a tradeoff between the exact count and using our approximation. However for larger problems, it is clearly very expensive to obtain the exact count. The tradeoff between efficiency and precision should be the guide for choosing between Cachet and LOBACS.